堆排序&优先级队列

二叉堆

本文主要参考二叉堆详解实现优先级队列。对其作者labuladong表示感谢。

说到二叉堆就不得不提到二叉树，在二叉树中有一种特殊的树叫做完全二叉树，而堆就是一种完全二叉树。因此，堆可以用数组来表示。因为完全二叉树的节点之间存在如下关系：

某个节点(其索引为k)的父节点的索引为(k / 2),其左孩子节点索引为2 k,右孩子节点为2 k + 1。正是因为这种关系，才可以用数组来表示堆。

如下图

注：数组的第一个索引 0 空着不用。因为数组索引是数组，为了方便区分，将字符作为数组元素。

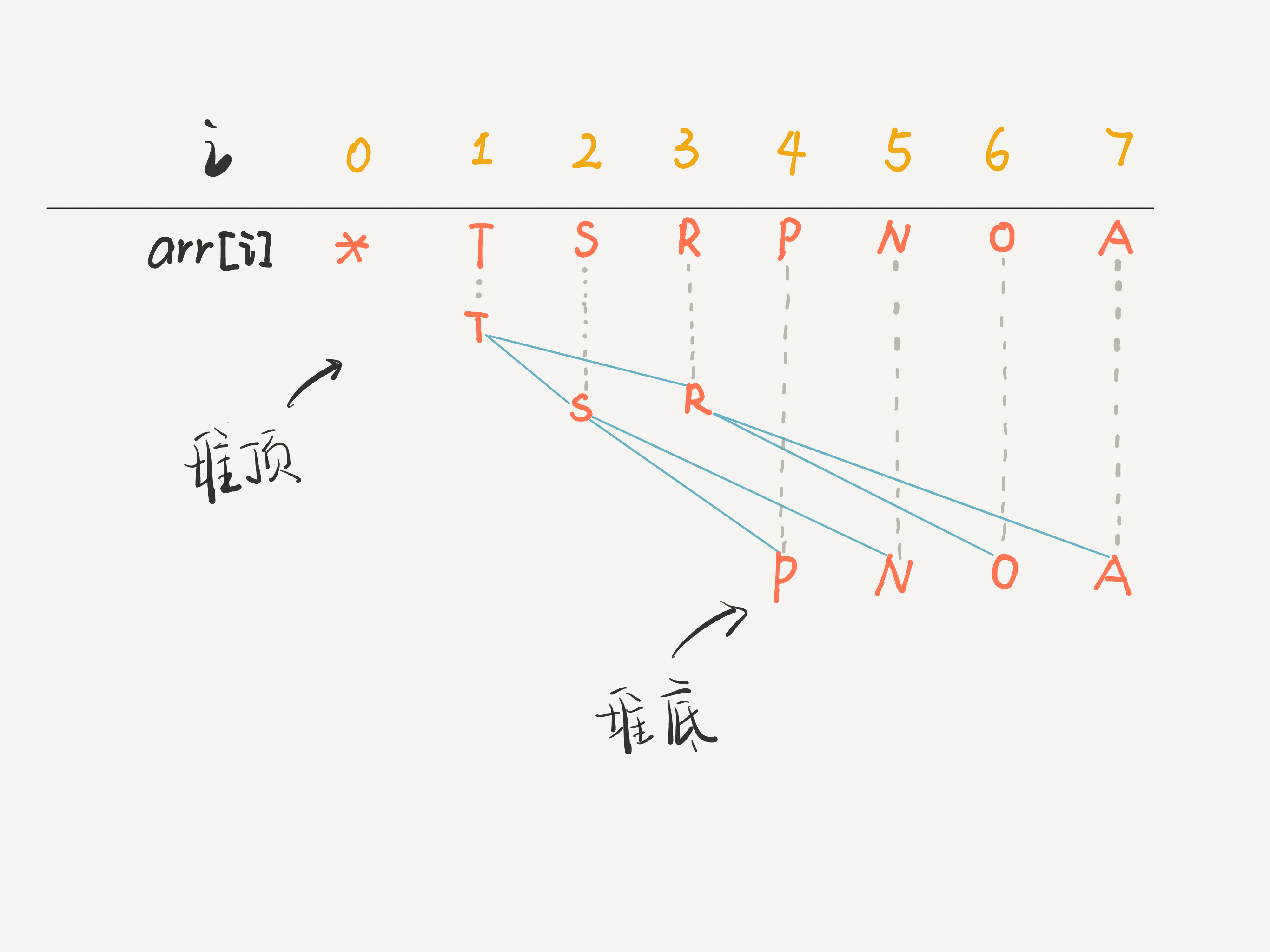
可以看到，把arr[1]作为整棵树的根的话，每个节点的父节点和左右孩子节点的索引都可以通过简单的运算得到。

二叉堆还分为最大堆(大顶堆)和最小堆(小顶堆)。最大堆的性质是：每个节点都大于等于它的两个子节点。类似的，最小堆的性质是：每个节点都小于等于它的子节点。

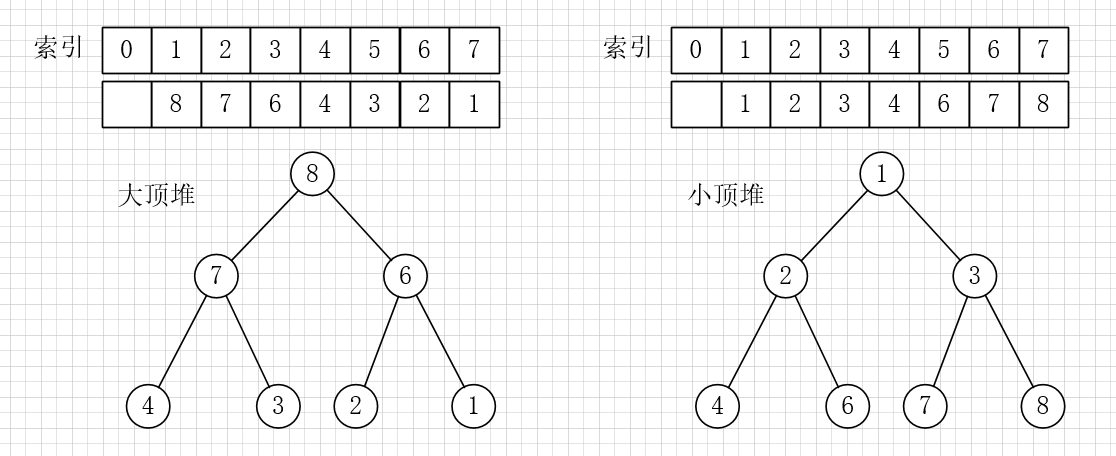
堆主要应用有两个, 首先是一种排序方法「堆排序」, 第二是一种很有用的数据结构「优先级队列」。

堆排序

在说堆排序之前，先要知道怎么建堆。常见的方式有两种：

• 插入式建堆：每次插入一个节点，实现一个大顶堆（或小顶堆）

  • 自下而上式堆化: 将插入节点与其父节点比较，如果插入节点大于父节点（大顶堆）或插入节点小于父节点（小顶堆），则插入节点与父节点调整位置。一直重复这一步，直到不需要交换或交换到根节点，此时插入完成。

• 原地建堆

  • 自下而上式堆化: 将节点与其父节点比较，如果节点大于父节点（大顶堆）或节点小于父节点（小顶堆），则节点与父节点调整位置.

  • 自上而下式堆化: 将节点与其左右子节点比较，如果存在左右子节点大于该节点（大顶堆）或小于该节点（小顶堆），则将子节点的最大值（大顶堆）或最小值（小顶堆）与之交换。

所以，自下而上式堆是调整节点与父节点（往上走），自上往下式堆化是调整节点与其左右子节点（往下走）。

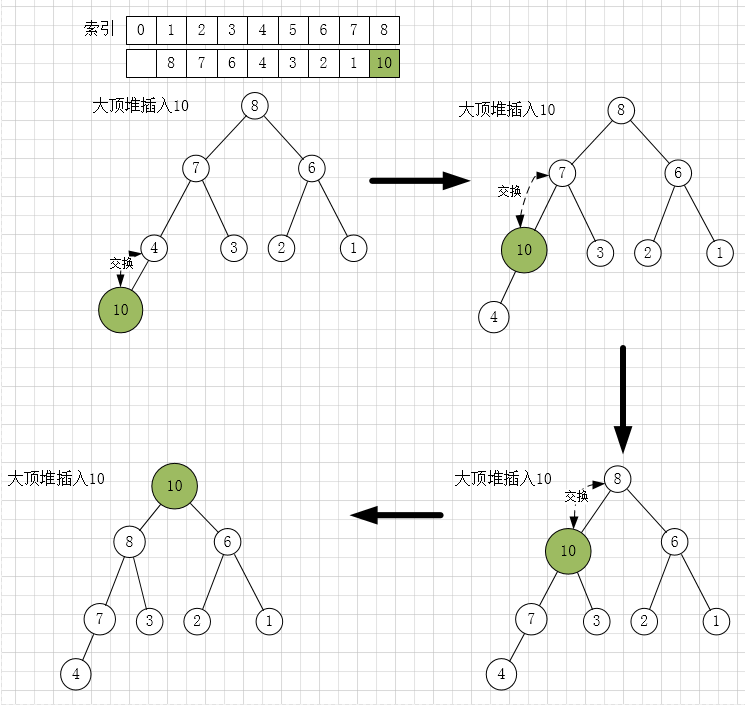
插入式建堆

插入节点：

• 将节点插入队尾
• 自下而上堆化
• 一直重复这一步，直到不需要交换或交换到根节点，此时插入完成。

代码实现(大顶堆)：

let item = [, 6, 5, 4, 1, 3, 2];
function insert(key) {
  item.push(key);
  let index = item.length - 1;
  while(index / 2 > 0 && item[index] > item[Math.floor(index / 2)]) {
    [item[index], item[Math.floor(index / 2)]] = [item[Math.floor(index / 2)], item[index]];
    index = Math.floor(index / 2);
  }
}

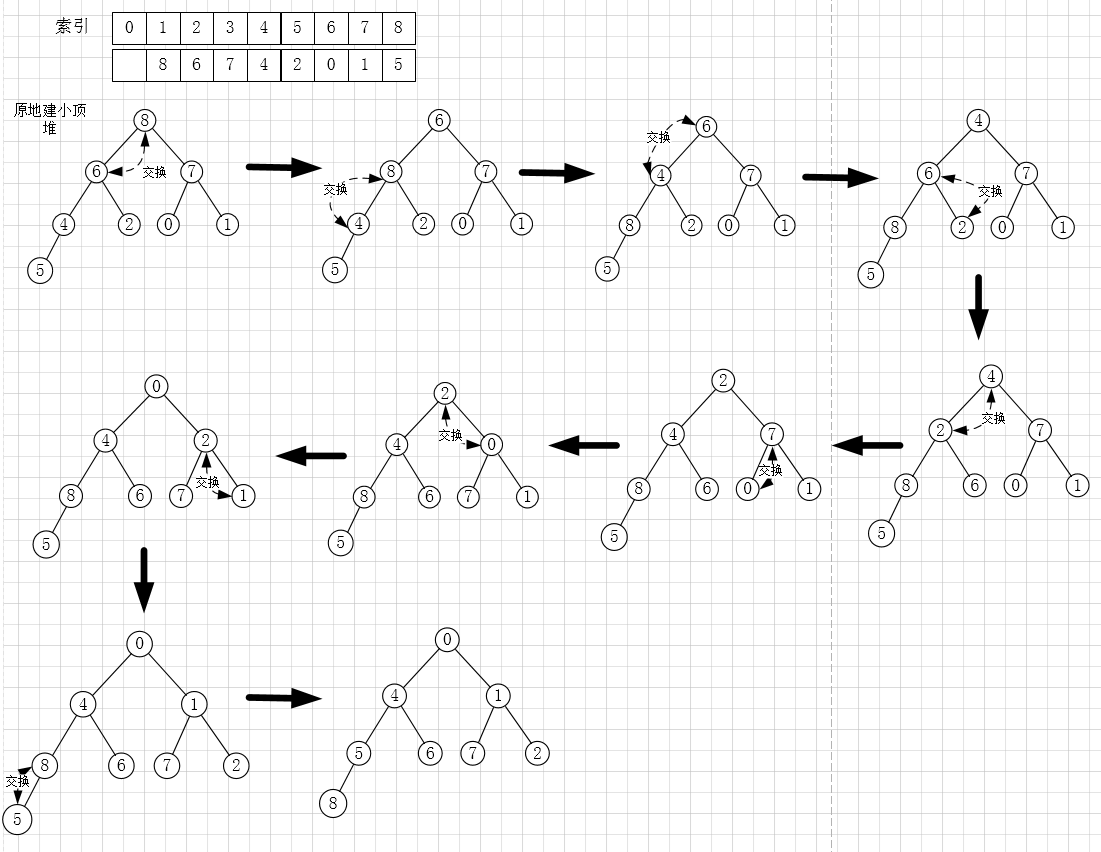
原地建堆

1. 从前往后、自下而上式堆化建堆

以小顶堆为例:

代码：

function buildHeap(arr, heapIndex) {
  while(heapIndex < arr.length - 1) {
    heapIndex++;
    heapify(arr, heapIndex);
  }
}
function heapify(item, i) {
  while(i / 2 > 0 &&　item[i] < item[Math.floor(i / 2)]) {
    [item[i], item[Math.floor(i / 2)]] = [item[Math.floor(i / 2)], item[i]];
    i = Math.floor(i / 2);
  }
}
let arr = [,8,6,7,4,2,0,1,5]
buildHeap(arr, 1);
console.log(arr); //[empty, 0, 4, 1, 5, 6, 7, 2, 8]

1. 从后往前、自上而下式堆化建堆

以小顶堆为例

注：从后往前并不是从序列的最后一个元素开始，而是从最后一个非叶子节点开始，这是因为，叶子节点没有子节点，不需要自上而下式堆化。

最后一个子节点的父节点为 n/2 ，所以从 n/2 位置节点开始堆化。

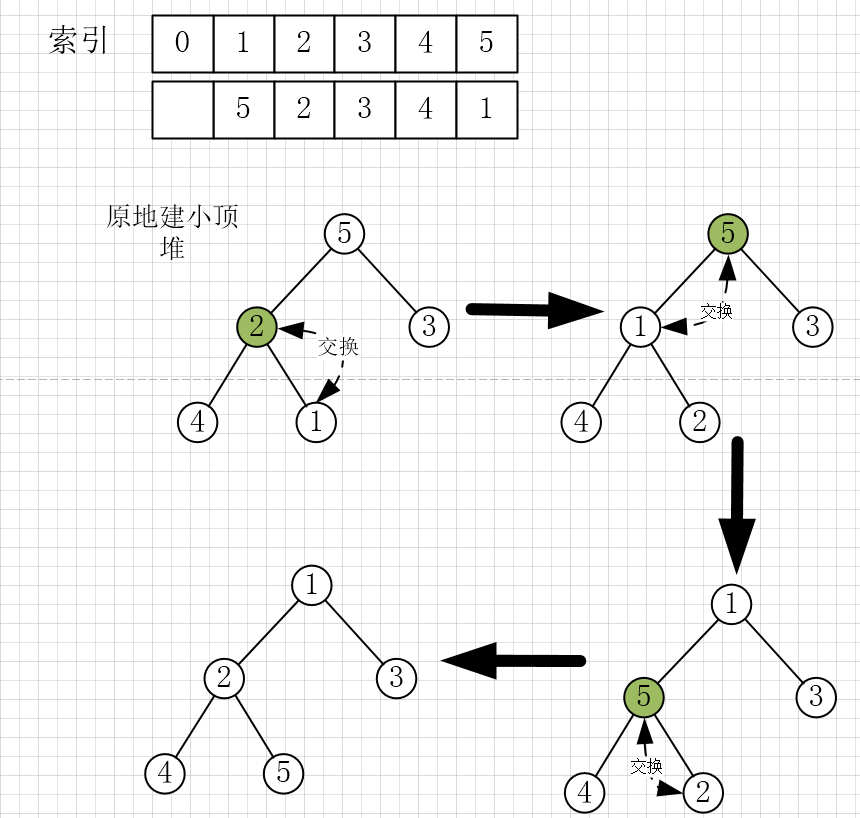
代码：

function buildHeap(arr, heapIndex) {
  for(let i = Math.floor(heapIndex / 2); i >= 1; i--) {
    heapify(arr, i, heapIndex);
  }
}
function heapify(item, i, size) {
  while(true) {
    let smallerIndex = i;
    if(2 * i <= size && item[i] > item[2 * i]) {
      smallerIndex = 2 * i;
    }
    if(2 * i + 1 <= size && item[smallerIndex] > item[2 * i + 1]) {
      smallerIndex = 2 * i + 1;
    }
    if(smallerIndex == i) break;
    [item[i], item[smallerIndex]] = [item[smallerIndex], item[i]];
    i = smallerIndex;
  }
}
let arr = [,5,2,3,4,1]
buildHeap(arr, arr.length - 1);

堆排序

• 原理

堆是一棵完全二叉树，它可以使用数组存储，并且大顶堆的最大值存储在根节点（i=1），所以我们可以每次取大顶堆的根结点与堆的最后一个节点交换，此时最大值放入了有效序列的最后一位，并且有效序列减1，有效堆依然保持完全二叉树的结构，然后堆化，成为新的大顶堆，重复此操作，知道有效堆的长度为 0，排序完成。

(升序)完整步骤为：

• 将原序列(n个)转化为一个大顶堆
• 设置堆的有效序列长度为n
• 将堆顶元素(第一个有效序列)与最后一个子元素(最后一个有效序列)交换，并且有效序列长度减一
• 再次堆化有效序列，使有效序列再次堆化为一个新的大顶堆
• 重复以上两步，直到有效序列的长度为1

代码：

function heapSort(arr) {
  buildHeap(arr, 1, 0);
  for(let i = 1; i < arr.length - 1; i++) {
    [arr[1], arr[arr.length - i]] = [arr[arr.length - i], arr[1]];
    buildHeap(arr, 1, i);
  }
}
function buildHeap(arr, heapIndex, size) {
  while(heapIndex < arr.length - 1 - size) {
    heapIndex++;
    heapify(arr, heapIndex);
  }
}
//自下而上堆化
function heapify(item, i) {
  while(i / 2 > 0 && item[i] > item[Math.floor(i / 2)]) {
    [item[i], item[Math.floor(i / 2)]] = [item[Math.floor(i / 2)], item[i]];
    i = Math.floor(i / 2);
  }
}
var items = [,1, 9, 2, 8, 3, 7, 4, 6, 5]
heapSort(items)
console.log(items);//[empty, 1, 2, 3, 4, 5, 6, 7, 8, 9]

TopK问题(leetcode215)

题目描述：

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

• 示例 1:

  输入: [3,2,1,5,6,4] 和 k = 2

  输出: 5

• 示例 2:

  输入: [3,2,3,1,2,4,5,5,6] 和 k = 4

  输出: 4

思路：

思路一：

• 构建大顶堆(假设有效长度为n = arr.length - 1)
• 将第一个元素与最后一个元素交换位置，然后有效长度减一(n-1)
• 再将有效长度减一(n-1)的序列进行大堆化，再将第一个元素与有效序列的最后一个元素交换。
• 重复k次，返回倒数第k个元素。

代码：

var findKthLargest = function (nums, k) {
  buildHeap(nums, 0, 0);
  for (let i = 0; i < k; i++) {
    [nums[0], nums[nums.length - i - 1]] = [nums[nums.length - i - 1], nums[0]]
    buildHeap(nums, 0, i + 1);
  }
  return nums[nums.length - k];
};

//原地建堆(大顶堆)
function buildHeap(arr, heapSize, size) {
  while (heapSize < arr.length - size - 1) {
    heapSize++;
    heapify(arr, heapSize);
  }
}

//自下而上
function heapify(item, i) {
  while (i / 2 > 0 && item[i] > item[Math.floor(i / 2)]) {
    [item[i], item[Math.floor(i / 2)]] = [item[Math.floor(i / 2)], item[i]];
    i = Math.floor(i / 2);
  }
}

思路二：

• 对前k个元素构建小顶堆
• 然后遍历第k个元素往后的所有元素，判断每个元素与小顶堆堆顶的大小
• 如果小于堆顶元素，啥也不做，直接下一个；如果大于堆顶的元素，则交换位置
• 然后将交换的元素下沉到正确的位置(后面会提到的优先级队列)。(或者对前k个元素再次进行小堆化)
• 返回堆顶元素。

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var findKthLargest = function (nums, k) {
  //对前k个元素进行小堆化
  buildSmallHeap(nums, 0, k);
  for(let i = k; i < nums.length; i++) {
    if(nums[i] > nums[0]) {
      [nums[i], nums[0]] = [nums[0], nums[i]];
      //buildSmallHeap(nums, 0, k);
      sink(nums, 0, k);
    }
  }
  return nums[0];
};


//原地建小顶堆
function buildSmallHeap(arr, heapSize, size) {
  while (heapSize < size - 1) {
    heapSize++;
    heapify_s(arr, heapSize);
  }
}

//自下而上
function heapify_s(item, i) {
  while (i / 2 > 0 && item[i] < item[Math.floor(i / 2)]) {
    [item[i], item[Math.floor(i / 2)]] = [item[Math.floor(i / 2)], item[i]]
    i = Math.floor(i / 2);
  }
}

//下沉(和左右孩子节点中的较小值交换位置)
function sink(nums, m, size) {
  while (true) {
    let samller = m;
    if (2 * m + 1 < size && nums[m] > nums[2 * m + 1]) {
      samller = 2 * m + 1;
    }
    if (2 * (m + 1) < size && nums[samller] > nums[2 * (m + 1)]) {
      samller = 2 * (m + 1);
    }
    if (m == samller) break;
    //exchange
    [nums[m], nums[samller]] = [nums[samller], nums[m]];
    m = samller;
  }
}

优先级队列

优先级队列这种数据结构有一个很有用的功能，你插入或者删除元素的时候，元素会自动排序，以维护堆的性质，这底层的原理就是二叉堆的操作。

数据结构的功能无非增删查该，优先级队列有两个主要 API，分别是 insert 插入一个元素和 delMax 删除最大元素（如果底层用最小堆，那么就是 delMin）。

下面我们实现一个简化的优先级队列，先看下代码框架：

class PQ {
  pqArr = [,]

  //返回当前队列中最大元素
  max() {
    return this.pqArr[1]
  }

  //插入元素num
  insert(num) {}

  //删除并返回当前队列中的最大元素
  delMax() {}
  
  //上浮第k个元素
  swim(k) {}

  //下沉第k个元素
  sink(k) {}
  
  //第k个元素父节点索引
  parent(k) {
    return Math.floor(k / 2);
  }

  //第k个元素左孩子节点索引
  left(k) {
    return 2 * k;
  }

  //第k个元素的右孩子节点索引
  right(k) {
    return 2 * k + 1;
  }

  //打印当前队列
  print() {
    console.log(this.pqArr);
  }
}

实现上浮 和 下沉(大顶堆为例)

为什么要有上浮 swim 和下沉 sink 的操作呢？为了维护堆结构。

我们要讲的是最大堆，每个节点都比它的两个子节点大，但是在插入元素和删除元素时，难免破坏堆的性质，这就需要通过这两个操作来恢复堆的性质了。

对于最大堆，会破坏堆性质的有有两种情况：

• 如果某个节点 A 比它的子节点（中的一个）小，那么 A 就不配做父节点，应该下去，下面那个更大的节点上来做父节点，这就是对 A 进行下沉。

• 如果某个节点 A 比它的父节点大，那么 A 不应该做子节点，应该把父节点换下来，自己去做父节点，这就是对 A 的上浮。

当然，错位的节点 A 可能要上浮（或下沉）很多次，才能到达正确的位置，恢复堆的性质。所以代码中肯定有一个 while 循环。

上浮的代码：

...
//上浮第k个元素
swim(k) {
  // 如果浮到堆顶，就不能往上浮了
  while (k > 1 && this.pqArr[k] > this.pqArr[this.parent(k)]) {
    //如果第k个元素大于其父元素，则交换它们的位置
    [this.pqArr[k], this.pqArr[this.parent(k)]] = [this.pqArr[this.parent(k)], this.pqArr[k]];
    k = this.parent(k);
    }
}
...

下层的代码实现：

下沉比上浮略微复杂一点，因为上浮某个节点 A，只需要 A 和其父节点比较大小即可；

但是下沉某个节点 A，需要 A 和其两个子节点比较大小，如果 A 不是最大的就需要调整位置，要把较大的那个子节点和 A 交换。

//下沉第k个元素
sink(k) {
  while (true) {
    let biggerIndex = k;
    if(this.left(k) < this.pqArr.length && this.pqArr[k] < this.pqArr[this.left(k)]) {
      biggerIndex = this.left(k);
    }
    if(this.right(k) < this.pqArr.length &&　this.pqArr[biggerIndex] < this.pqArr[this.right(k)]) {
      biggerIndex = this.right(k);
    }
    if(biggerIndex == k) break;
    [this.pqArr[k], this.pqArr[biggerIndex]] = [this.pqArr[biggerIndex], this.pqArr[k]];
    k = biggerIndex;
  }
}

至此，二叉堆的主要操作就讲完了。明白了 sink 和 swim 的行为，下面就可以实现优先级队列了。

实现delMax 和 insert

这两个方法就是建立在swim和sink基础上的。

insert方法先把要插入的元素添加到堆底的最后，然后让其上浮到正确的位置。

实现代码：

insert(num) {
  this.pqArr.push(num);
  this.swim(this.pqArr.length - 1)
}

delMax方法先把堆顶的元素A和堆底最后的元素B对调，然后删除A，最后让B下沉到正确的位置。

delMax() {
  let max = this.max();
  [this.pqArr[1], this.pqArr[this.pqArr.length - 1]] = [this.pqArr[this.pqArr.length - 1], this.pqArr[1]];
  this.pqArr.splice(this.pqArr.length - 1, 1);
  this.sink(1);
  return max;
}

至此，一个优先级队列就实现了，插入和删除元素的时间复杂度为 O(logK)，K 为当前二叉堆（优先级队列）中的元素总数。因为我们时间复杂度主要花费在 sink 或者 swim 上，而不管上浮还是下沉，最多也就树（堆）的高度，也就是 log 级别。

完整优先级队列代码：

class PQ {
  pqArr = [,]
  max() {
    return this.pqArr[1]
  }
  insert(num) {
    this.pqArr.push(num);
    this.swim(this.pqArr.length - 1)
  }

  delMax() {
    let max = this.max();
    [this.pqArr[1], this.pqArr[this.pqArr.length - 1]] = [this.pqArr[this.pqArr.length - 1], this.pqArr[1]];
    this.pqArr.splice(this.pqArr.length - 1, 1);
    this.sink(1);
    return max;
  }

  //上浮第k个元素
  swim(k) {
    while (k > 1 && this.pqArr[k] > this.pqArr[this.parent(k)]) {
      [this.pqArr[k], this.pqArr[this.parent(k)]] = [this.pqArr[this.parent(k)], this.pqArr[k]];
      k = this.parent(k);
    }
  }

  //下沉第k个元素
  sink(k) {
    while (true) {
      let biggerIndex = k;
      if (this.left(k) < this.pqArr.length && this.pqArr[k] < this.pqArr[this.left(k)]) {
        biggerIndex = this.left(k);
      }
      if (this.right(k) < this.pqArr.length && this.pqArr[biggerIndex] < this.pqArr[this.right(k)]) {
        biggerIndex = this.right(k);
      }
      if (biggerIndex == k) break;
      [this.pqArr[k], this.pqArr[biggerIndex]] = [this.pqArr[biggerIndex], this.pqArr[k]];
      k = biggerIndex;
    }
  }

  parent(k) {
    return Math.floor(k / 2);
  }

  left(k) {
    return 2 * k;
  }

  right(k) {
    return 2 * k + 1;
  }
  print() {
    console.log(this.pqArr);
  }
}
let pq = new PQ();
pq.insert(1);
pq.insert(8);
pq.insert(9);
pq.insert(0);
pq.insert(7);
pq.insert(5);
pq.insert(6);
pq.insert(10);
pq.insert(73);
pq.print();

console.log(pq.delMax());
pq.print();

console.log(pq.delMax());
pq.print();

最后总结

二叉堆就是一种完全二叉树，所以适合存储在数组中，而且二叉堆拥有一些特殊性质。

二叉堆的操作很简单，主要就是上浮和下沉，来维护堆的性质（堆有序）。

优先级队列是基于二叉堆实现的，主要操作是插入和删除。插入是先插到最后，然后上浮到正确位置；删除是调换位置后再删除，然后下沉到正确位置。