回溯算法及题目
| 题号 |
题目 |
Tag |
| 39 |
组合总和 |
数组、回溯算法 |
| 40 |
组合总和II |
数组、回溯算法 |
| 46 |
全排列 |
数组、回溯算法 |
| 51 |
N皇后 |
数组、回溯算法 |
墙裂推荐这篇文章:回溯算法解题套路框架
下面内容大多参考上面这篇文章,对其作者labuladong表示感谢。
回溯算法的框架
解决一个回溯问题,实际上就是一个决策树的遍历过程。 只需要思考3个问题:
- 路径:也就是已经做出的选择
- 选择列表:也就是当前可以做的选择
- 结束条件:也就是到达决策树底层,无法再做选择的条件。
在后面的题目中会对这个三个词语再进行解释。
代码方面,回溯算法的框架:
1
2
3
4
5
6
7
8
9
10
11
12
13
| let res = [];
function backtrack(路径, 选择列表) {
if(满足结束条件) {
res.add(路径);
return;
}
for (let 选择 in 选择列表) {
做选择
backtrack(路径, 选择列表)
撤销选择
}
}
|
其核心就是for循环里面的递归,在递归之前「做选择」,在递归之后「撤销选择」. 关于做选择和撤销选择,先通过全排列这个问题来了解一下。
全排列
我们知道n个不重复的数,全排列共有n!个。
为了简单清晰起见,这次只考虑全排列问题不包含重复的数字。
那么我们当时是怎么穷举全排列的呢?比方说给三个数 [1,2,3],你肯定不会无规律地乱穷举,一般是这样:
先固定第一位为 1,然后第二位可以是 2,那么第三位只能是 3;然后可以把第二位变成 3,第三位就只能是 2 了;然后就只能变化第一位,变成 2,然后再穷举后两位……
其实这就是回溯算法,我们高中无师自通就会用,或者有的同学直接画出如下这棵回溯树:
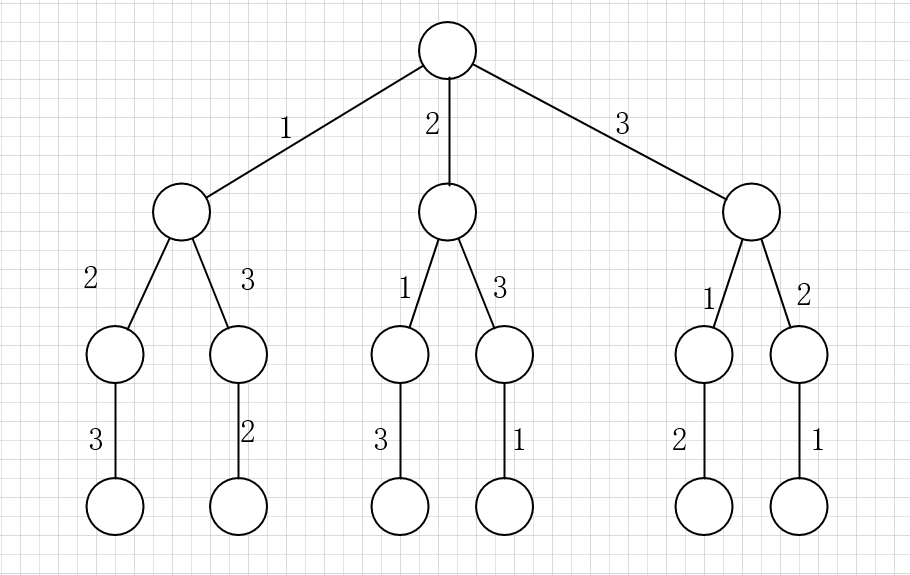
只要从根遍历这棵树,记录路径上的数字,其实就是所有的全排列。我们不妨把这棵树称为回溯算法的「决策树」。
为啥说这是决策树呢,因为你在每个节点上其实都在做决策。 比如你站在下图的红色节点上:
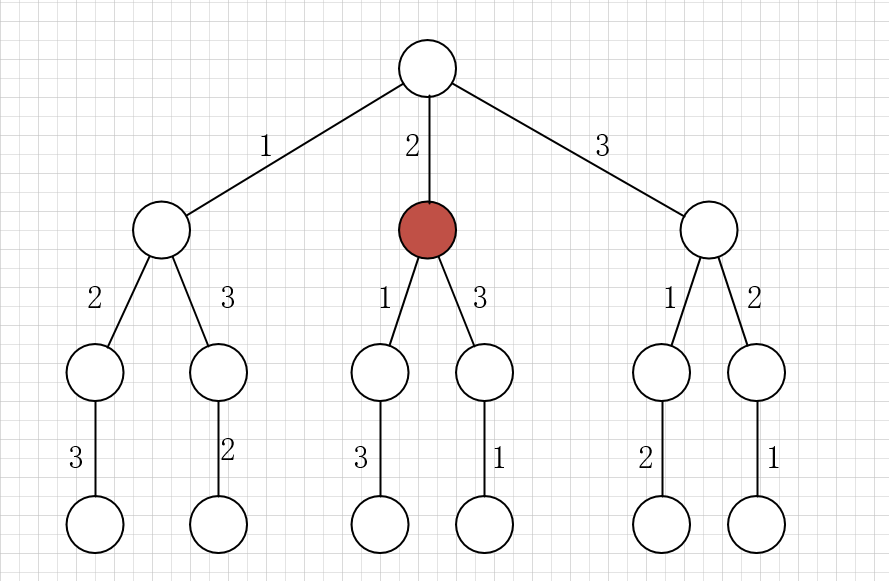
你现在就在做决策,可以选择 1 那条树枝,也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢?因为 2 这个树枝在你身后,这个选择你之前做过了,而全排列是不允许重复使用数字的。
现在就可以解答开头的几个名词:[2]就是「路径」,[1,3]就是「选择列表」,表示你当前可以做出的选择;「结束条件」就是遍历到树的底层,在这里就是选择列表为空的时候。
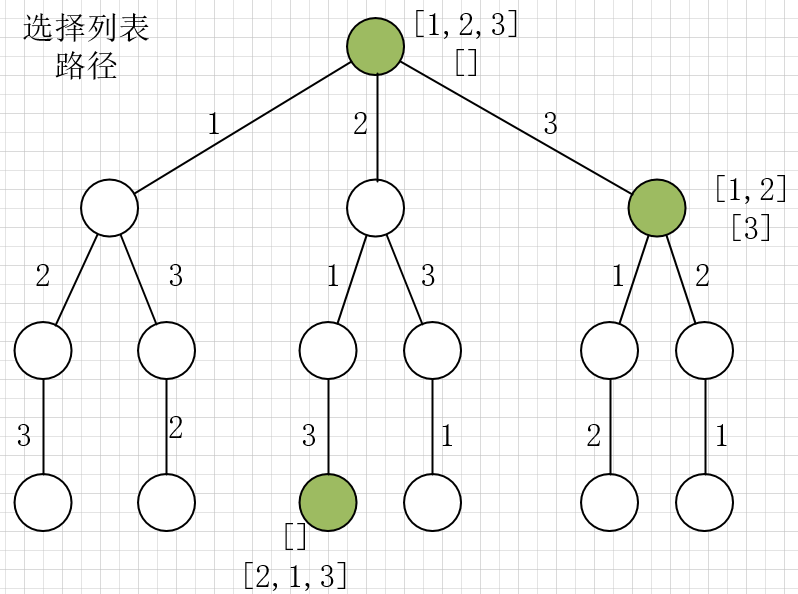
我们定义的backtrack函数其实就像一个指针,在这棵树上游走,同时要正确维护每个节点的属性,每当走到树的底层,其「路径」就是一个全排列。
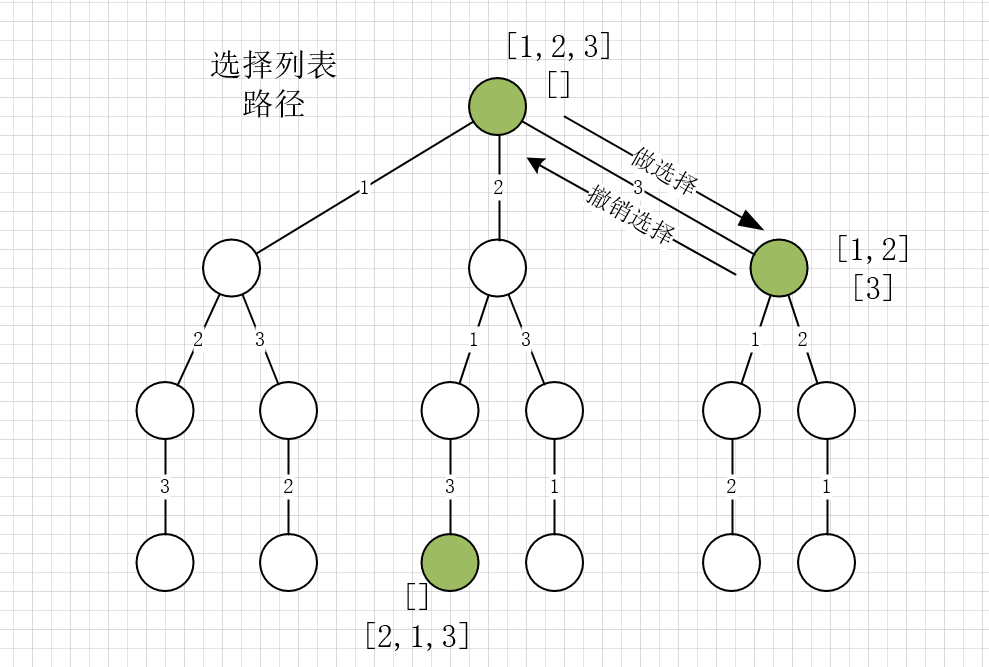
所以说for循环里面的递归就是回溯算法的关键:
1
2
3
4
5
6
| for 选择 in 选择列表
路径.push(选择)
backtrack(路径,选择列表)
路径.pop(选择)
|
我们只要在递归之前做出选择,在递归之后撤销刚才的选择,就可以正确地得到每个节点的选择列表和路径。
46、全排列代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
var permute = function (nums) {
let res = [], track = [];
if (nums.length == 0) return [];
backtrack(track);
function backtrack(track) {
if (track.length == nums.length) {
res.push(track.slice());
return;
}
for (let i = 0; i < nums.length; i++) {
if (track.includes(nums[i])) continue;
track.push(nums[i]);
backtrack(track);
track.pop();
}
}
return res;
};
|
我们这里稍微做了些变通,没有显式记录「选择列表」,而是通过 nums 和 track 推导出当前的选择列表:判断track.includes(nums[i])。
39、组合总和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
|
var combinationSum = function (candidates, target) {
let res = [], track = [];
candidates.sort((a, b) => a - b);
function backtrack(target, track, start) {
if(target == 0) {
res.push(track.slice());
return;
}
for(let i = start; i < candidates.length; i++) {
if(target < candidates[i]) break;
track.push(candidates[i]);
backtrack(target - candidates[i], track, i);
track.pop();
}
}
backtrack(target, track, 0);
return res;
}
|
40、组合总和II
这个和第39题的不同之处在于,数组中的元素可以重复, 并且每个数字在每个组合中只能使用一次。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
var combinationSum2 = function (candidates, target) {
let res = [], track = [];
candidates.sort((a, b) => a - b);
function backtrack(target, track, start) {
if(target == 0) {
res.push(track.slice());
return;
}
for(let i = start; i < candidates.length; i++) {
if(i - start > 0 && candidates[i - 1] == candidates[i]) continue;
if(target < candidates[i]) break;
track.push(candidates[i]);
backtrack(target - candidates[i], track, i + 1);
track.pop();
}
}
backtrack(target, track, 0);
return res;
}
|
51、N皇后
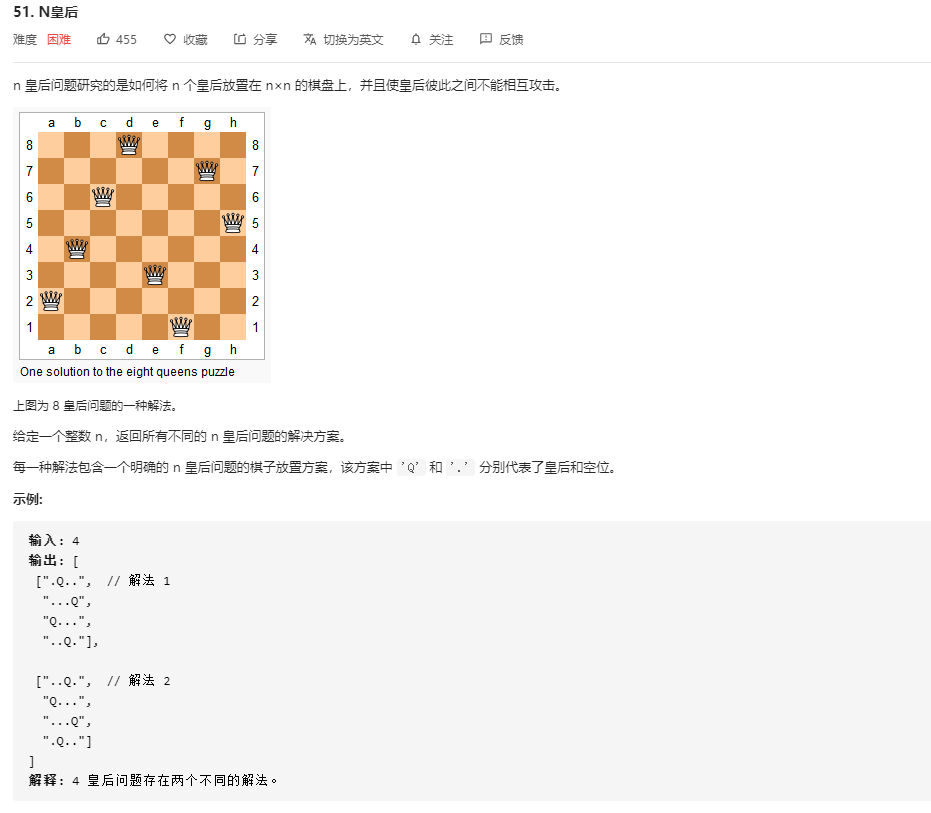
ps:皇后,是国际象棋中的棋子,意味着国王的妻子。皇后只做一件事,那就是“吃子”。当她遇见可以吃的棋子时,就迅速冲上去吃掉棋子。当然,她横、竖、斜都可走一到七步,可进可退。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
var solveNQueens = function (n) {
let res = [], board = [];
for(let i = 0; i < n; i++) {
board[i] = new Array(n).fill('.');
}
function backtrack(board, row) {
if(row == board.length) {
res.push(JSON.parse(JSON.stringify(board)));
return;
}
for(let column = 0; column < board.length; column++) {
if(!isValid(board, row, column)) continue;
board[row][column] = 'Q';
backtrack(board, row + 1);
board[row][column] = '.';
}
}
function isValid(board, row, column) {
for(let m = 0; m < board.length; m++) {
if(board[m][column] == 'Q') return false;
}
for(let m = row - 1, n = column + 1; m >= 0 && n < board.length; m--, n++) {
if(board[m][n] == 'Q') return false;
}
for(let m = row - 1, n = column - 1; m >= 0 && n >= 0; m--, n--) {
if(board[m][n] == 'Q') return false;
}
return true;
}
backtrack(board, 0);
return res.map(item => {
return item.map(subitem => subitem.join(''));
});;
}
|
最后
回溯算法就是个多叉树的遍历问题,关键就是在前序遍历和后序遍历的位置做一些操作,算法框架如下:
1
2
3
4
5
6
|
for (let 选择 in 选择列表) {
做选择
backtrack(路径, 选择列表)
撤销选择
}
|
写backtrack函数时,需要维护走过的「路径」和当前可以做的「选择列表」,当触发「结束条件」时,将「路径」记入结果集。










