漫话:如何给女朋友解释为什么计算机中 0.2 + 0.1 不等于 0.3 ?
漫话:如何给女朋友解释为什么计算机中 0.2 + 0.1 不等于 0.3 ?
背景
关于在计算机中 0.1 + 0.2 为什么不等于 0.3这个问题,以前确实很好奇。但是由于一些不可抗力(懒)一直没有去深挖下去。近日,偶然发现一篇文章漫话:如何给女朋友解释为什么计算机中 0.2 + 0.1 不等于 0.3 ?,通过漫画的形式对这个问题做了解释,醍醐灌顶,遂转载至博客。对其作者表示感谢。
下面时正文。
正文





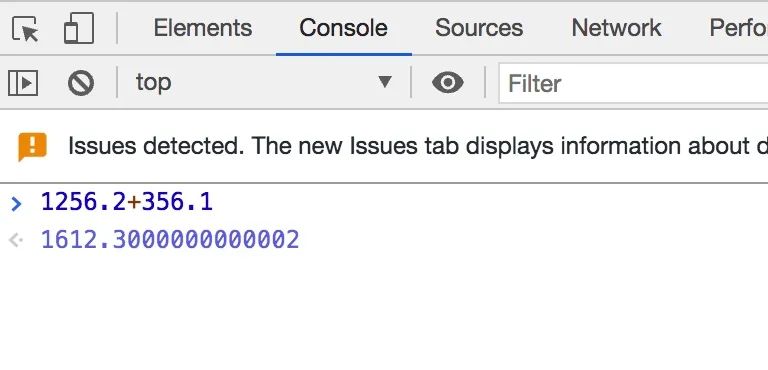






为什么当我们使用电脑浏览器计算0.2+0.1的时候,解决却是0.30000000000000004,而0.1+0.6的结果却是0.7呢?
这个问题其实一直是一个经典的问题,甚至有一个网站的域名就是https://0.30000000000000004.com/ ,主要就是解释这个问题的。
在这个网站中,列举了各种编程语言中计算0.2+0.1的结果,摘选几个如下:


可以看到,在各种语言中,计算0.2+0.1的结果都出奇的一致,那就是这个神奇的0.30000000000000004。
其实,当我们使用浏览器的控制台(F12)进行计算的时候,用到的就是JavaScript语言进行计算的,所以,前面的现象,归根结底其实和具体的编程语言无关。
主要问题还是计算机中到底是如何表示小数以及如何进行小数运算的。


我们知道,计算机只认识0和1 [为什么计算机只认识0和1],现实世界中的内容想要通过计算机存储、计算或者展示,都需要转换2进制。在现实世界中,数字主要有整数和小数两种。
在之前的[为什么计算机用补码存储数据]这篇文章中,我们介绍过,计算机中表示整数的方式有很多,如原码、反码以及补码等。
整数包括正整数、负整数以及零。在计算机中存储的整数则分为有符号数和无符号数。
对于无符号数,采用哪种编码方式都无所谓,对于有符号数的编码方式,常用的是补码。
那么,一个十进制数字想要获得其二进制的补码,需要先通过一定的算法得到他对应的原码。
反码是基于原码计算得来的,表示方式是:正数的反码是其本身。负数的反码是在其原码的基础上, 符号位不变,其余各个位取反。
如,10 的 原码为 0 1010 ,那么他的反码同样也是 0 1010 。
如,-2 的原码为 1 0010 ,那么他的反码为 1 1101 。
补码是在原码和反码的基础上衍生出来的,补码的表示方法是:正数的补码就是其本身,负数的补码是在其原码的基础上, 符号位不变, 其余各位取反,最后+1。(即在反码的基础上+1)
使用补码的原因:
- 计算机的运算器为了实现简单,倾向于在运算过程中将减法转换成加法,统一使用加法运算器进行计算。想要把减法转化成加法运算,就需要在运算时带着符号一起运算,而反码和补码可以带符号位一起运算,也就方便了将减法转换为加法。
- 采用补码,可以解决编码中有+0和-0两种表示0的方式。
十进制转二进制
首先我们看一下,如何把十进制整数转换成二进制整数?
十进制整数转换为二进制整数采用”除2取余,逆序排列”法。
具体做法是:
- 用2整除十进制整数,可以得到一个商和余数;
- 再用2去除商,又会得到一个商和余数,如此进行,直到商为小于1时为止
- 然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
如,我们想要把127转换成二进制,做法如下:

那么,十进制小数转换成二进制小数,又该如何计算呢?
十进制小数转换成二进制小数采用”乘2取整,顺序排列”法。
具体做法是:
- 用2乘十进制小数,可以得到积
- 将积的整数部分取出,再用2乘余下的小数部分,又得到一个积
- 再将积的整数部分取出,如此进行,直到积中的小数部分为零,此时0或1为二进制的最后一位。或者达到所要求的精度为止。

所以,十进制的0.625对应的二进制就是0.101。


不是所有数都能用二进制表示
我们知道了如何将一个十进制小数转换成二进制,那么是不是计算就可以直接用二进制表示小数了呢?
前面我们的例子中0.625是一个特列,那么还是用同样的算法,请计算下0.1对应的二进制是多少?

我们发现,0.1的二进制表示中出现了无限循环的情况,也就是(0.1)10 = (0.000110011001100…)2
这种情况,计算机就没办法用二进制精确的表示0.1了。
也就是说,对于像0.1这种数字,我们是没办法将他转换成一个确定的二进制数的。




IEEE 754
为了解决部分小数无法使用二进制精确表示的问题,于是就有了IEEE 754规范。
IEEE二进制浮点数算术标准(IEEE 754)是20世纪80年代以来最广泛使用的浮点数运算标准,为许多CPU与浮点运算器所采用。
浮点数和小数并不是完全一样的,计算机中小数的表示法,其实有定点和浮点两种。因为在位数相同的情况下,定点数的表示范围要比浮点数小。所以在计算机科学中,使用浮点数来表示实数的近似值。
IEEE 754规定了四种表示浮点数值的方式:单精确度(32位)、双精确度(64位)、延伸单精确度(43比特以上,很少使用)与延伸双精确度(79比特以上,通常以80位实现)。
其中最常用的就是32位单精度浮点数和64位双精度浮点数。
IEEE并没有解决小数无法精确表示的问题,只是提出了一种使用近似值表示小数的方式,并且引入了精度的概念。
浮点数是一串0和1构成的位序列(bit sequence),从逻辑上用三元组{S,E,M}表示一个数N,如下图所示:
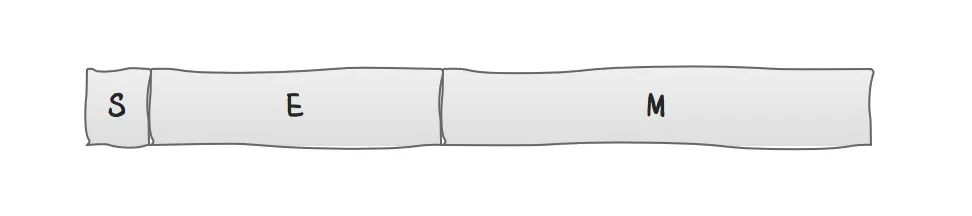
- S(sign)表示N的符号位。对应值s满足:n>0时,s=0; n≤0时,s=1。
- E(exponent)表示N的指数位,位于S和M之间的若干位。对应值e值也可正可负。
- M(mantissa)表示N的尾数位,恰好,它位于N末尾。M也叫有效数字位(significand)、系数位(coefficient), 甚至被称作”小数”。
则浮点数N的实际值n由下方的式子表示:
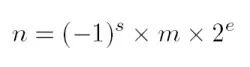
上面这个公式看起来很复杂,其中符号位和尾数位还比较容易理解,但是这个指数位就不是那么容易理解了。
其实,大家也不用太过于纠结这个公式,大家只需要知道对于单精度浮点数,最多只能用32位字符表示一个数字,双精度浮点数最多只能用64位来表示一个数字。
而对于那些无限循环的二进制数来说,计算机采用浮点数的方式保留了一定的有效数字,那么这个值只能是近似值,不可能是真实值。
至于一个数对应的IEEE 754浮点数应该如何计算,不是本文的重点,这里就不再赘述了,过程还是比较复杂的,需要进行对阶、尾数求和、规格化、舍入以及溢出判断等。
但是这些其实不需要了解的太详细,我们只需要知道,小数在计算机中的表示是近似数,并不是真实值。根据精度不同,近似程度也有所不同。
如0.1这个小数,他对应的在双精度浮点数的二进制为:0.00011001100110011001100110011001100110011001100110011001 。
0.2这个小数0.00110011001100110011001100110011001100110011001100110011 。
所以两者相加:

转换成10进制之后得到:0.30000000000000004!




避免丢失精度
在Java中,使用float表示单精度浮点数,double表示双精度浮点数,表示的都是近似值。
所以,在Java代码中,千万不要使用float或者double来进行高精度运算,尤其是金额运算,否则就很容易产生资损问题。
为了解决这样的精度问题,Java中提供了BigDecimal来进行精确运算。









